Polak o krok od rozwiązania słynnego problemu matematycznego P vs NP
Polak o krok od rozwiązania słynnego problemu matematycznego P vs NP
Nasi użytkownicy założyli 1 288 956 zrzutek i zebrali 1 519 713 861 zł
A ty na co dziś zbierasz?
Aktualności89

Dodawaj aktualności i informuj wspierających o postępach akcji.
To zwiększy wiarygodność Twojej zrzutki i zaangażowanie darczyńców.
Opis zrzutki
W 1998 odkryłem nową funkcję matematyczną (VMPC), która pozwala rozwiązać jeden z najsłynniejszych problemów matematycznych świata, P vs NP. Opublikowałem ją na międzynarodowej recenzowanej konferencji naukowej FSE w 2004.
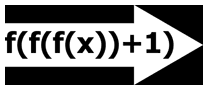
Obecnie, po 24 latach badań, kończę pisać pracę naukową (ponad 100 stron), która rozwiązuje problem P vs NP poprzez udowodnienie, że funkcja VMPC jest (pierwszą na świecie) funkcją jednokierunkową.
Zbieram na poprawę warunków życia, do jakich mnie to doprowadziło.
Przez 24 lata, które poświęciłem badaniom, straciłem wiele aspektów normalnego życia. Żadna instytucja nie ma procedur do finansowania projektu, który trwa tak długo. Finansuję badania indywidualnie, dzięki pomocy ludzi dobrej woli i prowadzeniu bardzo skromnego trybu życia. Mieszkam w wynajętej suterenie 30m2, jeżdżę 32-letnim samochodem (Toyota Corolla 1.3 rocznik 1990), którego blacharkę naprawiam własnoręcznie metodami chałupniczymi.
 Z góry dziękuję za każdą pomoc.
Z góry dziękuję za każdą pomoc.
Strona projektu: www.pieknafunkcja.pl

Artykuł w Gazecie Wyborczej "Wrocławianin na tropie zagadki tysiąclecia. Szyfry to jego specjalność"

Artykuł na portalu INN:Poland "Bartosz Żółtak twierdzi, że rozwiązał największą zagadkę matematyczną świata. Ubogi geniusz, który zmieni naukę?"
Wystąpienie na konferencji TEDx 2015:
W roku 2003, jako nikomu nieznana osoba, zgłosiłem pracę o odkrytej przez siebie funkcji VMPC na prestiżową międzynarodową recenzowaną konferencję naukową FSE. Praca została przyjęta do publikacji.
Byłem pierwszym Polakiem, który dostał się na tej rangi konferencję w branży.

Dofinansowanie na wyjazd otrzymałem od Kancelarii Prezydenta Rzeczpospolitej Polskiej, Aleksandra Kwaśniewskiego oraz od Prezydenta Wrocławia, Rafała Dutkiewicza.
W 2004 otrzymałem kilka propozycji pisania doktoratu na polskich uczelniach, ale wolałem kontynuować moje badania niezależnie.
Funkcja VMPC (Variably Modified Permutation Composition, czyli zmiennie modyfikowane złożenie permutacji) to nieopisane wcześniej nietypowe połączenie złożenia permutacji i operacji arytmetycznych, określone wzorem f(f(f(x))+1).
Najważniejszą własnością tej funkcji jest jej jednokierunkowość.
Jest to pierwsza na świecie funkcja jednokierunkowa.
Jednokierunkowość oznacza, że łatwo jest obliczyć wartość funkcji y=F(x), ale nie da się wykonać operacji odwrotnej - znaleźć argumentu x, z jakiego dana wartość y powstała.
Najważniejsze, że gdyby udało się formalnie udowodnić jednokierunkowość VMPC, rozwiązałoby to słynny problem matematyczny "czy P=NP?". Stwierdzeniem, że P ≠ NP.
"Czy P=NP?" to problem, który instytut matematyczny Clay Mathematics Institute w USA zaliczył do 7 największych nierozwiązanych problemów matematycznych świata, tzw. Problemów Milenijnych (Millennium Problems).
Obecnie jestem na samej końcówce zapisywania na czysto tego dowodu.
Tak, dowodu, że funkcja VMPC jest jednokierunkowa i że P ≠ NP.

Pomysłem na sfinansowanie moich badań było stworzenie gry planszowej Permutu

Jej mechanika odzwierciedla proces odwracania funkcji VMPC. Mimo matematycznych korzeni, gra jest niezwykle prosta i wciągająca. Wydałem ją samodzielnie za pożyczone od taty pieniądze (których cięgle nie oddałem). Mimo że gra podoba się graczom, to bez kosztownej machiny marketingowej nie da się dziś niczego sprzedać w większych ilościach. Sprzedaż Permutu jest symboliczna i nie wpływa odczuwalnie na moją sytuację finansową.
Inni niezależni naukowcy
Chciałbym podzielić się dwoma przykładami osób, które też poświęciły się nauce poza systemem akademickim, a mimo to osiągnęły wybitne wyniki.
Srinivasa Ramanujan, matematyk żyjący w latach 1887-1920 w Indiach, był naturalnym geniuszem, który bez formalnego wykształcenia zajmował się matematyką wyższą. W wieku 20 lat odciął się od systemu akademickiego i żyjąc w ekstremalnej biedzie, kontynuował swoje badania niezależnie. Samodzielnie sformułował mnóstwo niesamowitych twierdzeń matematycznych. 6 lat później został odkryty przez profesora Hardy'ego z Uniwersytetu Cambridge. Niestety, Ramanujan zmarł w wieku 32 lat na gruźlicę. Przez całe życie miał kłopoty ze zdrowiem, częściowo będące skutkiem niedożywienia, wynikającego z biedy. Prof. Hardy powiedział, że największym matematycznym osiągnięciem jego życia było odkrycie... Ramanujana.

Grigorij Perelman, który rozwiązał inny Problem Milenijny - udowodnił hipotezę Poincare'go - całkowicie odciął się od środowiska akademickiego i to mimo że z takim osiągnięciem każde drzwi stałyby przed nim otworem. Nie przyjął nawet nagrody instytutu Claya ani uważanego za matematycznego Nobla, Medalu Fieldsa. Jednocześnie samodzielnie rozwiązał problem, z którym żaden inny matematyk na świecie nie poradził sobie przez dziesiątki lat.

W długoterminowym rozrachunku największy pożytek z dorobku takich ludzi osiągają nie oni sami, ale społeczeństwo, które potem dorobek ten wykorzystuje.
Nieformalny blog z postępów pracy:
--------------------------------------------------------------------------------------
Więcej szczegółów o funkcji VMPC i problemie "czy P=NP?"
"Czy P=NP?" jest pytaniem, czy istnieją problemy, których rozwiązania nie da się łatwo znaleźć, ale których potencjalne rozwiązanie da się łatwo zweryfikować (sprawdzić, czy jest poprawne).
Jeśli istnieje funkcja jednokierunkowa, to znaczy, że problemy takie istnieją.
Oto, dlaczego:
Funkcja jest jednokierunkowa, gdy dla zadanego Y nie da się łatwo (czyli w czasie wielomianowym) znaleźć argumentu X, który po obliczeniu wartości funkcji, F(X), da zadaną wartość Y. Jednocześnie obliczenie wartości funkcji jednokierunkowej, F(X), dla zadanego argumentu X, jest łatwe (da się wykonać w czasie wielomianowym).
Odwracanie funkcji jednokierunkowej jest zatem problemem, którego rozwiązania nie da się łatwo znaleźć (nie da się znaleźć X na podstawie Y), a jednocześnie każde potencjalne rozwiązanie (X) da się łatwo zweryfikować, obliczając wartość funkcji, F(X), i porównując, czy uzyskany wynik jest równy zadanemu Y.
Formalnie powiemy, że problem odwracania funkcji jednokierunkowej (np. VMPC) należy do klasy problemów NP (dla których możliwe jest zweryfikowanie rozwiązania w czasie wielomianowym), ale nie należy do klasy problemów P (dla których możliwe jest znalezienie rozwiązania w czasie wielomianowym). Z tego wynika, że klasy problemów P i NP są różne (gdyż da się znaleźć problem, który należy do jednej klasy, ale nie należy do drugiej), czyli, zapisując formalnie, P ≠ NP.
Zatem, aby rozwiązać problem "czy P=NP?", wystarczy udowodnić, że jakaś funkcja (np. VMPC) jest jednokierunkowa.
Na razie nikomu nie udało się udowodnić jednokierunkowości żadnej funkcji. Jednocześnie wcześniej nie była znana funkcja VMPC. Jednokierunkowość zakorzeniona jest w samej istocie tej funkcji. Ja tylko miałem szczęście tę funkcję odkryć i ją zgłębić.
Czym dokładnie jest funkcja jednokierunkowa?
Jest to funkcja, której nie da się odwrócić. Co to znaczy? Dla przykładu, jeśli wiemy, że wartością funkcji X+1 jest liczba 11, to łatwo zauważyć, że X ma wartość 10 (bo 11 - 1 = 10). Korzystamy tu z faktu, że funkcją odwrotną do dodawania jest odejmowanie. Każda znana funkcja matematyczna posiada funkcję odwrotną. Mnożenie ma dzielenie, potęgowanie ma pierwiastkowanie, sinus ma arcus sinus, itd. Oprócz funkcji VMPC.
VMPC jest pierwszą na świecie funkcją, która nie posiada funkcji odwrotnej. Jest funkcją jednokierunkową. Jej sens można porównać do sytuacji, w której możemy dodać jedynkę do liczby X, ale nie możemy jej potem odjąć.
Dla interesujących się matematyką: Funkcję uznaje się za jednokierunkową, jeśli prawdopodobieństwo jej odwrócenia w średnim przypadku jest mniejsze niż odwrotność niewielomianowej (np. wykładniczej) funkcji wielkości problemu.
Dla ekspertów: Zamieszczam fragment mojej pracy, zawierający formalną definicję funkcji VMPC oraz funkcji jednokierunkowej:


Wybrane materiały prasowe

Wywiad w letnim numerze kwartalnika Przekrój, 2017

Artykuł o projekcie VMPC i grze Permutu, Młody Technik, styczeń 2015


Wywiad "Polskie krypto-odkrycie", magazyn komputerowy COMPUTERWORLD numer 8/612, 24.02.2004, strona 22


Artykuł "Funkcja jednokierunkowa i szyfr strumieniowy VMPC", magazyn komputerowy SOFTWARE 2.0 numer 9 (117), wrzesień 2004, strony 26-29

Wywiad dla Gazety Wyborczej, 13.02.2004, "Gazeta Wyborcza Wrocław", strona 2

Wywiad dla Gazety Wyborczej, 16.01.2004, "Wieża Ciśnień", strona 9


"Funkcja jednokierunkowa VMPC i system uwierzytelnionego szyfrowania VMPC-Tail-MAC". Krajowa Konferencja Zastosowań Kryptografii Enigma 2004, Warszawa, 10-13 maja 2004


"Rok w kryptoanalizie VMPC, schemat uwierzytelnionego szyfrowania VMPC-MAC oraz algorytm VMPC-HASH". Krajowa Konferencja Zastosowań Kryptografii Enigma 2005, Warszawa, 30 maja - 02 czerwca 2005

Wykład na Politechnice Krakowskiej p.t. "Historia pewnej jedynki. Od funkcji VMPC przez algorytm szyfrowania i problem, czy P=NP, do gry Permutu", 12.12.2013

Ta zrzutka nie ma jeszcze opisu.
Stwórz swój własny link do promocji zrzutki i sprawdzaj ile osób odwiedziło i wsparło tę zrzutkę z twojego polecenia! Dowiedz się więcej.
Stwórz swój własny link do promocji zrzutki i sprawdzaj ile osób odwiedziło i wsparło tę zrzutkę z twojego polecenia! Dowiedz się więcej.